�@
�����j���[
���l�m�[�g
2007.4�@�O�Y@int
1.���Ε]���Ƃ��Ă�
���l
2.���l�Ƃ͂ǂ�����
���̂�
3.��A�����Ɖ�A�W��
4.���W��
5.���_�̕��ς�
�W�����𐄒肷��
�@�[�I�ɂ͑��l�Ɣ�ׂ�]�����@�B�w�K�҂̑�����W�c�i�n��E�w�Z���E�w�N�Ȃǁj�̐��ѐ����i���ϓ_�E���ϓ��B�x�E���ϐ������Ȃǁj�Ɋ�Â��A�W�c�̒��Ōl�̐��т��ʒu�Â���]�����@�ł���B
�@�S���A���Ƃ�������K�͂ȏW�c�ɏ������Ċe���k�̑��ΓI�Ȋw�͂��v������ꍇ�ƁA�N���X��w�Z�ȂǁA��r�I�������W�c�������W�c�Ƃ���ꍇ������B���Ε]���͑傫�ȏW�c�̒��ŋq�ϓI�ł��邱�Ƃ�����Ƃ��Ă���A�����ȏW�c�ł���w�Z���⋳�����ł͏\���q�ϓI�Ƃ͂����Ȃ��B�����ȏW�c�̒��ł̈ʒu�t���́A���Q���o�Ă���B
�@�W�c�̐��ѕ��z�̈ʒu�W�ɂ��]�������܂邱�Ƃ��瑊�Ε]���Ƃ����B�u�W�c�ɏ��������]���v�Ƃ���������������B�q�ϓI�ŐM���������邪�A�q�����w�͂̓��e�ⓞ�B�̒��x����ł͂Ȃ��A�W�c�ł̈ʒu�W���炵���]�����Ȃ��Ƃ�������������B
�@�S�Ă̎q�ǂ��̊w�͕ۏ�Ƃ��������痝�O�Ƃ͖��W�ȕ]�����@�ł���Ƃ����w�E������B���̂悤�Ȕᔻ�����邱�Ƃ𗝉�������ŁA���Ε]���k�̋q�ϓI�Ȋw�͂𑪂�ړI�Ɍ��肵�ė��p����A�L���ȕ]�����@�ƂȂ邱�Ƃ������ł���B
�@���Ε]���́A���v�w�̐��K���z�Ɋ�b�������]���@�������̗p�����B���K���z�Ȑ��Ɋ�Â��T�i�K��P�O�i�K�]���ȂǂƂ��ė��p�����B���K���z�͐g����̏d�Ȃǂ̎��R�I�Ȍ��ۂ̑���x�����z�ȂǂɌ�����ޏ��^�̕��z�`��ŁA�w�͓��_������ɓK�p�������̂ł���B
�@�i�K�]���Ɛ��K���z�Ƃ̊W��}�ɂ���Ǝ��̂悤�ɂȂ�B
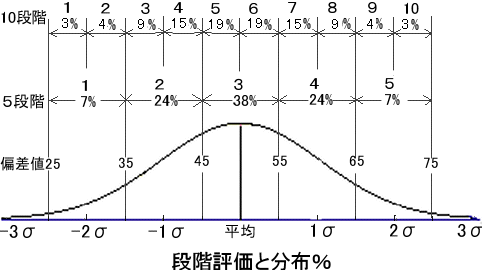
�@���K���z�̂������́A�W�����ɂ�芮�S�ɊǗ������Ƃ������������B�W�c���ψ�Ȃ�A�N���W�������Z�o���A�W������P�ʂƂ��ĕ]�����Ă��A��{�I�ɓ������ʂ�������B��������q�ϐ��ƐM�������ۏ����B
�@�e�����̕��ς���̕����悵�đ��a�����߂ĕ��ς��o���A����ɂ��̕����������߂�ƕW�����ɂȂ�B�W�����̓Ёi�V�O�}�j�ł���킳���B������u�T�i�K�]���v�͂P�ВP�ʂŋ��A�u�P�O�i�K�]���v��0.5�ВP�ʂŋ��B���z�S�̂�+-2.5�Ђ͈̔͂ŕ\���������̂ł���B
�@���K���z�́A +-1�Ђ̊Ԃɂ�����m����68.25%�A+-2�Ђ̊Ԃɂ�����m����95.45%�ƂȂ�A+-3�Ђ̊Ԃɂ�����m����99.73%�ƂȂ�B
�@�u���l�v�͈�ʂɁA51�i�K�]����0.1�Ђ�P�ʂƂ��Ă���A�����Ղ����邽�߁u�~10�{50�v�̉��H�����������̂������B���ς̈ʒu�����l50�ŁA���75�A����25���炢�ɂȂ�B���_�ƕ��ςƂ̍��Ɂu�~10�v����̂́A�����₷���悤�ɐ��������邽�߂ł���A�u+50�v����͕̂��ς̈ʒu���u50�v�Ƃ��邽�߂ł���B
�@���l��Z�l�Ƃ������邪�A���̎��Ōv�Z����B
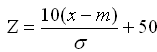 �@�@�@�ix�͌X�̓��_�Am�͕��ρA�Ђ͕W�����j
�@�@�@�ix�͌X�̓��_�Am�͕��ρA�Ђ͕W�����j
�@�w�Z����c�̓��̊e���Ȃ̊w�͕��l�́AExcel���̕\�v�Z�\�t�g���g���A�e�ՂɎZ�o�ł���B�ꐔ�ƂȂ链�_�ɂ��ĕ��ϓ_�ƕW�������v�Z���Ă����A�X�̓��_����̎��ɓ��Ă͂߂�A���l�͎Z�o�ł���B
�@���̂悤�ɕ��l�́A�w�͂𑪂���@�Ƃ��āA���̐����ɂ��e�Ղɋ��߂邱�Ƃ��ł���q�ϓI�ȕ]���@�Ƃ��čL�����y���Ă���B
�@���Ε]���́A�w�͕]���@�Ƃ��Ď��̂悤�Ȍ��_������Ƃ�����B�����̓����܂�����Ŏg�p����K�v������B
�i�P�j�u�S�Ă̎q�ǂ��̊w�͕ۏ�v�Ƃ������O�ɔ�����\��������B�q�������ɂǂ�Ȋw�͂������̂����킩��Ȃ��B�w�K�ڕW�ɑ���B���̒��x���킩��Ȃ��B
�i�Q�j��������u�e�X�g�ɍ��킹�ċ�����E�w�ԁv�\�����łĂ���B
�ǂ������͕ʂƂ��āA�e�X�g�̏o��͈͂��W�����ĕ�����A���̂��߂ɕ�����B�ǂ����т��Ƃ邱�Ƃ��w�K�̓��@�t���ƂȂ��Ă���ʂ�����B
�i�R�j�ڕW�̒B���x�f�������A�K�������p�ӂ���Ă���킯�ł͂Ȃ��B���Ε]���́A�]�����̂��̂Ƃ��ẮA�w���ڕW�ł���w�K���e�ɑ��铞�B���x�͕]�����Ȃ��B
�i�S�j�l���̕ω���c������̂ɂ͕s�����ł���B���ɁA�����Ȋw�Z���Ƃ����W�c�̒��ł͐��т̐L�т�]��������Ȃ��Ƃ�����肪����B
�i�T�j�����S�͕K�v�����A�K�v�ȏ�ɂ�����\��������Ƃ�����B
����ɂ��ւ�炸�A���k�̓K�x�ȋ����ƌ���S�ɑi���邱�ƂŁA�w�K�Ɍ����킹���@�t���ƂȂ���ʂ�����B
�@�����̓����܂�����Ŋ��p����Ȃ�A�K�ɗ��p����Ε��l�͗L���ȕ]�������ƂȂ�B�w�K�ڕW�K���ɑ��铞�B�x��ϓ_�ʂ̕]���́A���l�Ȃǂ̑��Ε]���Ƃ͕ʂɗp�ӂ��ׂ����̂ł��邱�Ƃ͂䂤�܂ł��Ȃ����낤�B
�@
�@���Ε]���̓T�^�I�ȕ]���@�Ƃ��Ģ���ϓ_�Ƃ̔�r���u���_���z�O���t�v��u���ʁv�Ȃǂ�����B���l�����̑�\�ł���B���l�́A���K���z�̗��_���e�X�g���_��т̕��z�ɓK�p���āA���ς���ǂ̒��x����Ă��邩���A���̓��v�ʂŕ\�������̂ł���B���l�́Az(Z)���_�Ƃ������B�u�W�����_�v�ƌ���������������B
�@�ϗʂ��ǂ̂悤�ɎU����Ă��邩�ׂ���@�Ƃ��āA�e�ϗʂ̕��ς���̊u���肪�傫�������������ׂ���@������B�e�ϗʂƕ��ς̍����u���v�Ƃ����B���ꂼ��̕����Q�悵�ĉ����ĕ��ς����߂邱�ƂŁA�f�[�^�̎U���̒��x��������B������u���U�v�Ƃ����B
�@���U�̐��̕��������u�W�����v(Standard Deviation =SD) �Ƃ����B���ς̎���ւ̃f�[�^�̎U��肪�傫����ΕW�����͂��������Ȃ�A�U��肪�������ق�0�ɋ߂Â��B
�W�����̌v�Z��
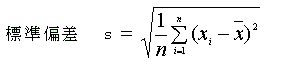
�@�W���I�ȃe�X�g�̐��т̏ꍇ�͕��ϓ_�̋߂��̐l������ԑ����A�O�_��100�_�ɋ߂Â��قǐl�������Ȃ��Ȃ�A���E�Ώ̂̒ޏ��^�ɂȂ邱�Ƃ������B���̂悤�ȕ��z�O���t�̌`���u���K���z�v�Ƃ����B
���K���z�̃O���t
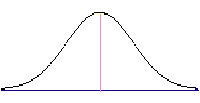
�@�W�������������ƁA���ς̎���Ƀf�[�^�͏W�����A���̂悤�Ȍ`�ɂȂ�B�t�ɕW�����i�Ёj���傫���ƁA�f�[�^�͕��ς��痣��ĕ��U���邱�ƂɂȂ�B�W�����́A���ς̎���ւ̎����̕��z�̏�Ԃ�\���A������R���g���[�����Ă���Ƃ�������B
�W�������������ꍇ�A���ς̎���Ɏ������W������B
 �@
�@
�@�W�������傫���ꍇ�A�����̕��z���Ⴂ��`�̎R�ɂȂ蕽�ς��痣��镪�z�ɂȂ�B���z�̎R��2�ɕ����ꂽ�肢�тɂȂ����肷�邱�Ƃ�����B

�@100�_���_�̃e�X�g�ł́A�W������20�O�オ�W���I�Ȓl�ŁA 15���炢�ɂȂ�Ə������B�����̓��_�����ς̎���ɂ��Ȃ�W�����Ă��邱�Ƃ�\���Ă���B�t�ɁA�W������25��30�ɂȂ�ꍇ������B�f�[�^�̕��U���傫�����Ƃ�\���A���т��ǂ����k�ƈ������k�ɕ�����Ă���ꍇ��A���z���㉺�ɑ�`��ɂȂ��Ă���ꍇ�ł���B
�@���K���z�́A���̂悤�Ȑ���������B
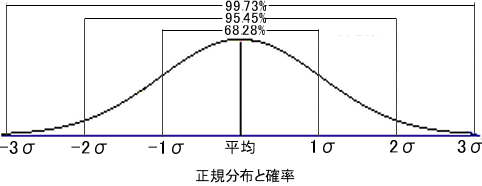
�@�܂�A����+-2.5�`3.0�W�����̊ԂɁA�w�ǂ̐��т����z���邱�ƂɂȂ�B
�@���̐�����i�K�]���ɉ��p����Ǝ��̂悤�ɂȂ�B
�@�q�ϕ]���̂T�i�K�]����10�i�K�]���́A���̐��K���z�̗��_�ɂ��B
�@���K���z�ƒi�K�]��

�@�W������P�ʂƂ����]���l���y�X�R�A�Ƃ������Ƃ�����B���ϒl����̗������x��W�����Ŋ��������̂ŁA���̎��ŕ\�����B
�@z=(��������_-���ϓ_)/�W����
�@5�i�K�]��͂��̂����_����Ƃ��Ă���B����́A���ς𒆐S�ɂ��ĕ��z�S�̂��T�W�����ŕ������A�e�W�����i�K�ɊY������ʐςz�S�̂�100%�ɑ���䗦�Ƃ��Ă���킵�����̂ł���B
�����_�ƂT�i�K�]���̊W�͎��̂Ƃ���B
| �W�����͈̔� | �i�K�@�@���z�� |
| -1.5�Јȉ� | 1�@(�S�̂�7%) |
| -1.5�`-0.5�� | 2�@(�S�̂�24%) |
| -0.5�`0.5�� | 3�@(�S�̂�38%) |
| 0.5�`1.5�� | 4�@(�S�̂�24%) |
| 1.5�Јȏ� | 5�@(�S�̂�7%) |
�@�y�l�́A-2.0�`�{2.0���炢�܂ŏ����t���ŕ\�������B����ł͈�ʂɎg���]���l�Ƃ��Ă͈����Â炢�̂ŁA���̂悤�ɉ��H���Ďg�����Ƃ������B�@
�@Z���_������ɍו������Ďg���₷�������]���l�����l�ŁA�T�i�K�̕]���������1/10�ɕ����������̂ŁA50�i�K�]���Ƃ�������B50�𒆐S�Ƃ���25�`75���x�̂�50�i�K�]���Ƃ��Ă���킳��邱�Ƃ������B�P�O�O�i�K�ɕ��������]��������悤���B
���l(Standard Score=SS)�̌v�Z��
�@Z(=SS) = 50 + 10�~(��������_ �| ���ϓ_)�^�W����
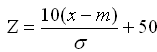 �@�@�ix�͓��_�Am�͕��ϓ_�A�Ђ͕W�����j
�@�@�ix�͓��_�Am�͕��ϓ_�A�Ђ͕W�����j
�@���l�́A����W�c�̃e�X�g���ʂƂ��Ă̓��_�ɂ��āA���ϓ_�ƕW���������߂���Όv�Z�ŋ��߂邱�Ƃ��ł���B �iExcel�Ȃ�A���_�̕��ϓ_�ƕW���������ꂼ��
AVERAGE���ASTDEV�W���� �����g�p���ċ��߂�B�j
�@���̎��ɂ��A���ϓ_�Ɠ������_�Ȃ���l��50�ɂȂ�B���_�����ϓ_��������x�ɉ�����51�E52�E53�E�E�E�Ƒ����A���75����80���炢�A���_�����ϓ_���������x�ɉ����āA49�E48�E47�E�E�E�ƂȂ�A����25���炢�܂ŁB
�@�Ⴆ�A100�_���_�̃e�X�g�ŁA���ϓ_��50�A�W������20�Ƃ���ƁA50�_�͕��l50�A100�_�͕��l75�A0�_�͕��l25�ƂȂ�B
�@��̎��ŁA���q�̓��_�ƕ��ϓ_�Ƃ̍���10�{����Ƃ������Ƃ́A����̕W������1/10��P�ʂƂ���Ƃ������ƂŁA1���l�͂̓��_���͕W������1/10�ƂȂ�B�W������20�Ƃ������Ƃ́A1���l�ɊY�����链�_��2�_�Ƃ������ƂɂȂ�B
�@���l�Ȃǂ̑��Ε]���́A���k�̊w�͂����ϓ_�̂܂��ɒޏ���ɕ��z���A100�_���_�̃e�X�g�ł͕��ϓ_=50�_�A�W����=20�̂Ƃ��ɁA0�_�����l25�A100�_�����l75�ƂȂ�A���ꂢ�ɕ]�����邱�Ƃ��ł���B
�@�����A���ۂ̃e�X�g��肪���̂悤�ɍ���邱�Ƃ͋H�ŁA�����͕��ϓ_������������Ⴉ������A���_���z�̌`���肪��������Q�ɕ��z�����ꂽ�肷��B
�@���{����e�X�g�̎�ނɂ����B���ԁE�����e�X�g�Ȃǂ̓����I�e�X�g�̏ꍇ�ɁA���l�ړx�͓K�����邪�A���P�����Ƃ̃e�X�g�͓��B�x�e�X�g�̏ꍇ�������A���ϓ_��70�`80�_�ɂȂ邱�Ƃ������B���̂悤�ȃe�X�g�ɕ��l�ړx��K�p���邱�Ƃɂ͖���������B���l���ړx�Ƃ���e�X�g�́A���ϓ_�͒����l50�_�ɂȂ邱�Ƃ�z�肵�Ă���A���̂��߂ɂ͂�����x�̕W�����̍�Ƃ��K�v�ɂȂ�B
�@���̏ꍇ�̕W�����Ƃ́A���̂悤�ȗv���������B
�@ �ݖ�̐��������������̂ƒႢ����(�o��̓�Փx)���o�����X�悭�z�u����A��b�I�o��Ɖ��p�I�E���W�I�o��̃o�����X�Ƃ����Ă��悢�B
�A�o��͈͂ƂȂ�w�K�̈悩��܂�ׂ�Ȃ��o�肷��B
�B�o��`���Ƃ��āA�I�����⌊���ߎ������łȂ��L�q���̊������l������B�̓_�̏����������Ȃ玩�R�L�q�Ȃǂ��̗p����B
�@���_���z�͐��K���z���Ă��Ȃ��̂ɁA�������l�̎ړx���g���đ������ꍇ�A���̎ړx�͐��m�Ƃ����邩�ǂ����B���_���z�ɓK�p�������l�́A���Ƃ��Ƃ���قnj����Ȏړx�ł͂Ȃ��B�W�c�����ł���A�e�X�g�̉���Ă��A�����̓�Փx�̕ϓ��������Ă��A�W�c�̂Ȃ��ł̈ʒu�Â��̎ړx�Ƃ��ăe�X�g���Ƃ̕��l���r���Ă݂邱�Ƃ��ł���A�Ƃ������x�ł���B���_���z�����K���z���Ă���ꍇ�Ɍ���A���Ƃ��Ε��l65�Ȃ��ʂ���7%�̈ʒu�Ƃ������Ƃ��ł��邪�A���ۂɂ͂����łȂ��ꍇ�������̂�����A���l�ɂ��W�c���̈ʒu���͑�܂��Ȑ���l�Ƃ������ƂɂȂ낤���B���_���z�����K���z���Ă��邩�ǂ����͂��Ă����Ƃ��āA���K���z���Ă���Ɖ��肵�ĕW������P�ʂƂ����ړx���A�Љ�̒��Ō����I�ȗL�����������Ă��邩�ǂ��������Ȃ̂ł���A���l�͈����x���̖������ʂ����Ă���Ƃ�����̂ł͂Ȃ����B
�@�w�Z����m�����̒c�̓��ł���A�\�v�Z��ȈՃf�[�^�x�[�X������A�W�c�̒��̕��ϓ_��W�������v�Z���A��L�̕��l�v�Z�̎��ɓ��Ă͂߂�A�N�ł��p�ӂɕ��l���Z�o���邱�Ƃ��ł���B�ł́A�n��S�̂�S���A����ɑS�����x���ł̕��l�̎Z�o�͂ǂ�����Čv�Z����̂��B
�@�S�����W�v�ł���Ή������Ȃ����A�����̃T���v���ł����S�����_���T���v�����O��A���i�K���o�Ȃǂ��ł���悢���A���ۂɂ͌���ꂽ�T���v�����琄�肹����Ȃ����Ƃ�����B�܂��A�O��̃e�X�g�ł̕��l�ƍ���̃e�X�g�ł̕��l�����܂�㉺�������ł͐M�������Ȃ��Ȃ�B���т̎ړx�Ƃ��Ă̐M�����ƈ��萫���K�v�ɂȂ�B
�@�L��e�X�g�ɂ����ẮA��������c�̂��S�����̃e�X�g�ɎQ������Ƃ������Ƃ͂܂�ł���B���肳�ꂽ�Q�����̕��ϓ_��W��������A�ǂ����ΑS�̂�(��W�c��)���ϓ_�ƕW�������Z�o���邱�Ƃ��ł���̂��B���ɁA�ߋ��̐��тƑ��ւ̂���T���v�������W�c�̕��ς�W�����𐄒肷����@���������Ă݂�B
�@
3.��A�����Ɖ�A�W��
�@X�̒l�����܂�A����ɑΉ�����Y�̒l�����܂�Ƃ����W���uY��X�̊��ł���v�Ƃ����B
�@Y=aX+b�@�̎������藧�Ƃ��A�uY��X�̈ꎟ���ł���v�Ƃ����BX��Y�͒����I�ȊW�ɂ���AX�����܂��Y���K�R�I�Ɍ��܂��Ă��܂��B
�@2�̕ϗ�X�AY������AX�̒l�����܂��Y�̒l���K�R�I�Ɍ��܂�Ƃ����킯�ł͂Ȃ����A���炩�̊W�����F�߂���ꍇ�A�uX��Y�̊Ԃɂ͑��֊W������v�Ƃ����B
�@���֊W�ɂ����낢��Ȍ`������B���̑��ւ�����Ε��̑��ւ�����B�Ȑ��I�ȊW��������B�܂����W�Ƃ����W�������邾�낤�B
�@�����ł͉��̐}�̂悤�ȁA���̑��ւŒ����I�ȊW�����F�߂��鑊�֊W���l����B
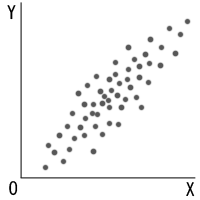
�@�Ⴆ�A�w���ɐ��w�̓��_�AY���ɗ��Ȃ̓��_���Ƃ�A���w�ʼn��_�Ƃ����l�͗��Ȃʼn��_�Ƃ����Ƃ����悤�Ƀv���b�g���Ă����B����Ə�̐}�̂悤�Ȑ}���o���オ��B���w�Ɨ��Ȃ̑��֕��z�ɒ����Ă͂߁A���̈ꎟ�������琔�w�̓��_���痝�Ȃ̓��_�𐄒肷��Ƃ������@������B
�@�ł����Ă͂܂�̂悢���������߂���@�Ƃ��āu�ŏ�����@�v������B���̕��@�ɂ��A �ꎟ����Y=aX+b�ɂ�����a��b�̒l�����߂邱�Ƃ��ł���B
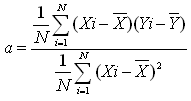 �@���̎���
�@���̎���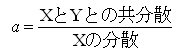 �Ƃ���킷���Ƃ��ł���B
�Ƃ���킷���Ƃ��ł���B
![]()
�@a�́uY��X�ւ̉�A�W���v�A���̒������uY��X�ւ̉�A�����v�Ƃ����B
�@���̒����́A���_�i![]() �A
�A![]() �j��ʂ�AX���ɑ���X����a�ƂȂ�B
�j��ʂ�AX���ɑ���X����a�ƂȂ�B
�@�����X����Y�𐄒肷��Ƃ��̎������AY����X�𐄒肵�����ꍇ������B���̏ꍇ�A���������g�����Ƃ͏o���Ȃ��B���̎��Ōv�Z����B
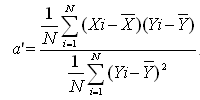 ���̎���
���̎���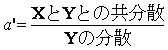 �Ƃ���킷���Ƃ��ł���B
�Ƃ���킷���Ƃ��ł���B
![]()
�@a�́uX��Y�ւ̉�A�W���v�A���̒������uX��Y�ւ̉�A�����v�Ƃ����B
�@
�@Y��X�ւ̉�A������X��Y�ւ̉�A�������A�U�z�}�̏�Ɉ����Ă݂�Ǝ��̂悤�ɂȂ�B
�@���̂Q�̒����͂Ƃ��Ɍ��_ �i![]() �A
�A![]() �j��ʂ�B
�j��ʂ�B
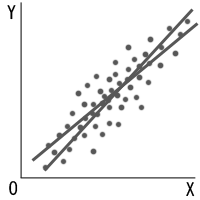
�@���̂Q�{�̒������d�Ȃ�̂́A���ւ����S�ȏꍇ�����B
�@�Q�{�̒����̉�A�W��a��a'�̊��ς��A���W��r�ɂȂ�B
�@����r���s�A�\���̕��ϗ����W���Ƃ����B
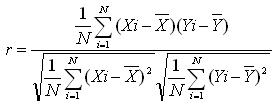 �@
�@
�@���W���̈Ӗ��͂����ł͐G��Ȃ��B
�@r���g���ĉ�A�W����\���Ǝ��̂悤�ɂȂ�B
�@Y��X�ւ̉�A�W���́A
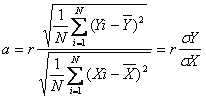
�@X��Y�ւ̉�A�W���́A
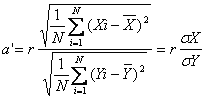
�@���W��r��X�̕W�����EY�̕W�������v�Z����Ă���Ȃ�A��A�W��a�����߂�ɂ͕ʓr�Ɍv�Z�����肱�̎����g�������֗��B
�@
�@��̉�A���̍l��������ɁA���ւ���u�O��̕��l�v�Ɓu����̓��_�v����A���_�́u���ϓ_�v�Ɓu�W�����v�𐄒肷�邱�Ƃ��ł���B���ɁA�u���ϓ_�v�Ɓu�W�����v�𐄒肷���@�ɂ��ĊT�v���������B
�@�O��̕��l�Ƃ̑��ւ��獡��̃e�X�g���_�̕��ϓ_�ƕW�����𐄒肷��ƁA�O��̕��l�Ɠ��l�̈Ӗ��Â��������ϓ_�ƕW�����𐄒肷�邱�Ƃ��ł���B�܂��A����̃e�X�g�̃T���v�������Ȃ��Ă��A���̃T���v���f�[�^�̉ߋ��̐��������l������������Ȃ�A����e�X�g�̕��ϓ_�ƕW�����邱�Ƃ��ł���B���Ȃ��T���v���f�[�^�ł����������փf�[�^������Ȃ�A���Ȃ萳�m�ɍ���e�X�g�̕�W�c�ɂ����镽�ϓ_�ƕW�����邱�Ƃ��ł��邫��߂Č����I�ŗL���ȕ��@�ł���B
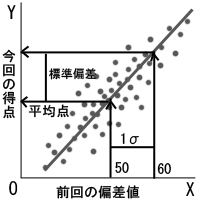
�@�O��̕��l��x���A����̓��_��y���ɂƂ�A���̎U�z�}���C���[�W����B�@
�@�O��̕��l50�̈ʒu����A��A�����𗘗p���č��_�̕��ϓ_�𐄒肷�邱�Ƃ��ł���B
�@Y=aX+b�@�̎���X=50�Ƃ���Y�����߂�ƁA���ꂪ���蕽�ϓ_�ƂȂ�B
�@�܂��A1�W�����̑傫���܂���l50������l60�܂ł̊Ԃ̕��ɑΉ�����Y�̕������߂�ƁA���ꂪ���_��1�W�����̑傫���ƂȂ�B
�@���_�̐��̕��ϓ_��W�����͗e�ՂɌv�Z���邱�Ƃ͂ł��邪�A�O��Ȃ����ߋ��̐���������ꂽ���l���v�Z���邽�߂̎����͂��邱�Ƃ��ł��Ȃ��B���̂悤�ȏꍇ�ɁA���̉�A������p���邱�Ƃŏ��Ȃ��T���v���̍��_����A��W�c�̕��ϓ_�ƕW�����𐄒肷�邱�Ƃ��ł���B
�@���̂悤�ȕ��@�ŋ��߂��A����e�X�g�̕��ϓ_�ƕW�������g���āA����e�X�g�̓��_�̕��l�t�����s�Ȃ����̑Ó�����]�����邱�Ƃ��ł���B���ƂŏW�v���邱�Ƃ͖����Ȃ̂ŁA�v���O������g��ŏW�v���邱�ƂɂȂ�B�O��̕��l��10�i�K���z���쐬��������O���t�\������B����ɁA����̐��蕽�ϓ_�Ɛ���W�������g�p����10�i�K���z���쐬���ăO���t�\������B����ƑO����l�̕��z�ɑ��āA������l�̕��z��Βu���Ĕ�r����B�������邱�ƂŁA����̕��ϓ_�ƕW�����̑Ó������ۏ���邱�ƂɂȂ�B
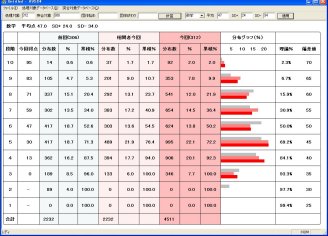
�@����̕��l���O��̕��l�Ɣ�r���āA10�i�K���z�̃o�����X�������ꍇ�A���肵�����ϓ_��W�������C�����邱�ƂŁA���l���z�̃o�����X�����邱�Ƃ��ł���B���蕽�ϓ_��W������ύX���āA�ď������s�ł���悤�Ƀv���O������g�ނƂ悢���낤�B
�@�W�����̏C���̃q���g�Ƃ��āA�W������傫������ƁA���l���z�ϋ߂��Ɉ�������ʂ�����B�t�ɕW����������������ƁA���l���z�ς�������������ʂ�����B
�@�ЂƂ̎����̕��z�͂ЂƂ̕W�����������A����I�ɕW�����̑傫�����Z�b�g���Čv�Z���邱�Ƃ��\�ł���B�Ⴆ�A���ϓ_����̕W�����̑傫���ƁA���ϓ_��艺�̕W�����̑傫����ς���Ƃ������삪�����I�ł���B
�@���ϓ_��80�_���x�ƍ����A�܂����ϓ_��肸���Ɖ���20�_�Ȃǂɂ����z������ꍇ�A���ϓ_����̕��l�v�Z�Ɏg�p����W���������������A���ϓ_��艺�̕��l�v�Z�Ɏg�p����W������傫�����邱�ƂŁA���l���z�̃o�����X��������x����邱�Ƃ��ł���B
�@���ϓ_��20�_���x�ƒႭ�A�܂����ϓ_��肸���Ə��80�_�Ȃǂɂ����z������ꍇ�A���ϓ_����̕��l�v�Z�Ɏg�p����W������傫�����A���ϓ_��艺�̕��l�v�Z�Ɏg�p����W���������������邱�ƂŁA������x����邱�Ƃ��ł���B
�@���l�͂��낢��Ȍ��_�������Ȃ�����A�w�͂̋q�ϓI�ȑ��莑���Ƃ��Č����̗L�����������Ă���B���l�̋q�ϐ���ۏ�����̂Ƃ��āA������̎����ɂ��Ă��̕��ϓ_�ƕW���������߁A������g���ČX�̓��_��������l�Ɋ��Z���邱�Ƃ��ł��A�N�ł����قړ����悤�Ȍ��ʂ��o�����Ƃ��ł���A�Ƃ������Ƃ���������B

�@
���v�Ɋւ���Q�l�����́A��Ɏ��̎����ɂ��B
�u�S������@���v�w�v��c�쒼�E���J���q�E���M�� ���� �|����